Answer:
![\boxed{c. \ f^(-1)(x)=\frac{1}{\sqrt[3]{x}}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/j9uiagfpvngvpauoyg9cn8m0pihata5909.png)
Explanation:
Let's find the inverse function of
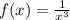 to know what item we must choose as correct. So let's apply this steps:
to know what item we must choose as correct. So let's apply this steps:
a) Use the Horizontal Line Test to decide whether
 has an inverse function.
has an inverse function.
As shown in the graph below there is no any horizontal line that intersects the graph of
 at more than one point. Thus, the function is one-to-one and has an inverse function. Therefore, the inverse is a function..
at more than one point. Thus, the function is one-to-one and has an inverse function. Therefore, the inverse is a function..
b) Replace
 by
by
 in the equation for
in the equation for
 .
.
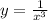
c) Interchange the roles of
 and
and
 and solve for
and solve for

![x=(1)/(y^3) \\ \\ \therefore y^3=(1)/(x) \\ \\ \therefore y=\frac{1}{\sqrt[3]{x}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/2cwmzagtub9lnx6wa8yebwcrqrcc0ghn08.png)
d) Replace
 by
by
 in the new equation.
in the new equation.
![f^(-1)(x)=\frac{1}{\sqrt[3]{x}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/o9hqqggqcdx7lg4oeqebeqvzxfxhexq516.png)
So the correct option is:
![c. \ f^(-1)(x)=\frac{1}{\sqrt[3]{x}}](https://img.qammunity.org/2020/formulas/mathematics/high-school/h7arzmjwmzuy924r03adshin39i77l8fwi.png)