Question

True or false

(Picture provided)

Answer 1

False.

Explanation:

We have given a function and its inverse:

f(x) = (x-3)³+4 and f⁻¹(x) = -3+∛ (x+4)

We have to find is it inverse of function or not.

We have given a function:

f(x) = (x-3)³+4

let f(x) = y we get,

y = (x-3)³+4

Interchange the place of x and y we get,

x= (y-3)³+4

(y-3)³ = x-4

y-3 = ∛ x-4

y = ∛ x-4 +3

Replacing y to f⁻¹(x) we get,

f⁻¹(x) = ∛ x-4 +3

The inverse of given function is f⁻¹(x) = ∛ x-4 +3.Which is different from the given inverse.

So, it is false.

Answer 2

False

Explanation:

Let's find the inverse function of
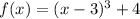`f(x)=(x-3)^3+4` to know whether this function has an inverse function
`f^(-1)(x)=-3+\sqrt[3]{x+4}`. So let's apply this steps:

a) Use the Horizontal Line Test to decide whether
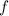`f` has an inverse function.

Given that f(x) is a cubic function there is no any horizontal line that intersects the graph of
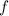`f` at more than one point. Thus, the function is one-to-one and has an inverse function.

b) Replace
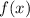`f(x)` by
`y` in the equation for
`f(x)`.

`y=(x-3)^3+4`

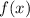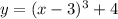
c) Interchange the roles of
`x` and
`y` and solve for
`y`

`x=(y-3)^3+4 \\ \\ \therefore x-4=(y-3)^3 \\ \\ \therefore (y-3)^3=x-4 \\ \\ \therefore y-3=\sqrt[3]{x-4} \\ \\ \therefore y=\sqrt[3]{x-4}+3`

d) Replace
`y` by
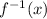`f^(-1)(x)` in the new equation.

`f^(-1)(x)=\sqrt[3]{x-4}+3`

So this is in fact the inverse function and it isn't the same given function. Therefore, the statement is false