Answer with explanation:
We are given a function f(x) in terms of variable x as:

- We know that a transformation of a parent function f(x) of the type:
f(x) → a f(x)
is either a vertical stretch or a shrink depending on a.
If a>1 then the transformation is a vertical stretch and if a<1 then it is a vertical squeeze.
- Also, the transformation of the type:
f(x) → f(ax)
is a horizontal stretch if a<1 and a horizontal shrink if a>1.
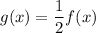
This means that the function g(x) is a vertical shrink of the parent function f(x) since a=1/2 <1
- Also, we can represent our function as:
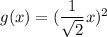
This means that:
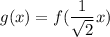
Here we have: a=1/√2 <1
This means that it is a horizontal stretch.