Question

Use Synthetic Division to Factor the following polynomials completely by given factors or roots and Find all the zeros; When you reach quadratic equation, performance regular factoring or Quadratic Formula.


`x^(5) -9x^(3) -x^(2) +9;(x-3),(x-1)`, as factors and -3 as a root

Answer 1

The factors are (x - (1 - i√3)/2) , (x - (1 + i√3)/2) , (x - 3) , (x + 3) , (x - 1)

The zeroes are 1 , 3 , -3 , (1 - i√3)/2 , (1 + i√3)/2

Explanation:

`(x^(5)+0-9x^(3) -x^(2)+0+9)` ÷ (x - 3) =

`(x^(4)-9x^(3)-x^(2)+0+9)` ÷ (x - 3) =

`x^(4)+3x^(3)+(-x^(2)+0+9)` ÷ (x - 3) =

`x^(4)+3x^(3)-x+(-3x+9)` ÷ (x - 3) =

`(x^(4)+3x^(3)-x-3)`

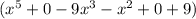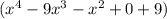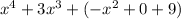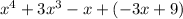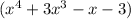
`(x^(4)+3x^(3)+0-x-3)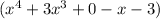` ÷ (x - 1) =

x³ + (4x³ + 0 - x - 3) ÷ (x - 1) =

x³ + 4x² + (4x² - x - 3) ÷ (x - 1) =

x³ + 4x² + 4x + (3x - 3) ÷ (x - 1) =

x³ + 4x² + 4x + 3

∵ -3 is a root ⇒ (x + 3) is a factor

(x³ + 4x² + 4x + 3) ÷ (x + 3) =

x² + (x² + 4x + 3) ÷ (x + 3) =

x² + x + (x + 3) ÷ (x + 3) =

x² + x + 1 ⇒ use the formula to find the factors of this quadratic

∵ a = 1 , b = 1 and c = 1

∴
`x=\frac{-1+\sqrt{(1)^(2)-4(1)(1)} }{2(1)}=(-1+√(-3))/(2)=(-1+i√(3))/(2)`

∴
`x=(-1-i√(3) )/(2)`

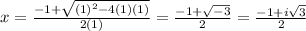
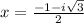
∴ The factors are (x - (1 - i√3)/2) , (x - (1 + i√3)/2) , (x - 3) , (x + 3) , (x - 1)

The zeroes:

x - 3 = 0 ⇒ x = 3

x + 3 = 0 ⇒ x = -3

x - 1 = 0 ⇒ x = 1

x - (1 - i√3)/2 = 0 ⇒ x = (1 - i√3)/2

x - (1 + i√3)/2 = 0 ⇒ x = (1 + i√3)/2

The zeroes are 1 , 3 , -3 , (1 - i√3)/2 , (1 + i√3)/2