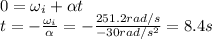Answer:
8.4 s
Step-by-step explanation:
First of all, let's convert the initial angular velocity of the engine from rpm into rad/s:
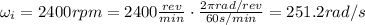
The angular velocity at time t is given by:
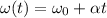
where
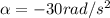 is the angular acceleration, which is negative because the engine is slowing down
is the angular acceleration, which is negative because the engine is slowing down
We want to know how long it takes for the drive to stop turning: this is equivalent of calculating the time t at which the angular velocity becomes zero,
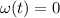 . Using the equation above, we have:
. Using the equation above, we have: