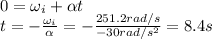Question

you pull your car into your driveway and stop. the drive shaft of your car engine, initially rotating at 2400rpm, slows with a constant rotational acceleration of magnitude 30 rad/s^2. How long it take for the drive to stop turning?

Answer 1

8.4 s

Step-by-step explanation:

First of all, let's convert the initial angular velocity of the engine from rpm into rad/s:

`\omega_i = 2400 rpm = 2400 (rev)/(min) \cdot (2\pi rad/rev)/(60 s/min)=251.2 rad/s`

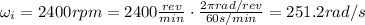
The angular velocity at time t is given by:

`\omega(t)= \omega_0 + \alpha t`

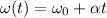
where

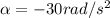`\alpha=-30 rad/s^2` is the angular acceleration, which is negative because the engine is slowing down

We want to know how long it takes for the drive to stop turning: this is equivalent of calculating the time t at which the angular velocity becomes zero,
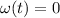`\omega(t)=0`. Using the equation above, we have:

`0=\omega_i + \alpha t\\t=-(\omega_i)/(\alpha)=-(251.2 rad/s)/(-30 rad/s^2)=8.4 s`