Question

(HELP ASAP) Use numerals instead of words.

What is the equation of the parabola passing through the points 2,3 , 6,9and 8,0?

Answer 1

Answers:

• -1 in the first box
• 19/2 or 9.5 in the second box
• -12 in the third box

=================================================

Work Shown:

We'll use the template y = ax^2 + bx + c

• If (x,y) = (2,3) is on the parabola, then y = ax^2+bx+c turns into 3 = a(2)^2 + b(2) + c. That simplifies to 4a+2b+c = 3
• If (x,y) = (6,9) is on the parabola, then y = ax^2+bx+c turns into 9 = a(6)^2 + b(6) + c. That simplifies to 36a+6b+c = 9
• If (x,y) = (8,0) is on the parabola, then y = ax^2+bx+c turns into 0 = a(8)^2 + b(8) + c. That simplifies to 64a+8b+c = 0

The system of equations is

`\begin{cases}4a+2b+c = 3\\36a+6b+c = 9\\64a+8b+c = 0\end{cases}`

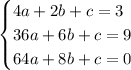
We have 3 equations and 3 unknowns.

-----------------------------------

Let's solve the first equation for c

4a+2b+c = 3

2b+c = 3-4a

c = 3-4a-2b

c = -4a-2b+3

Plug that into the second equation and simplify

36a+6b+c = 9

36a+6b+(-4a-2b+3) = 9

32a+4b+3 = 9

32a+4b = 9-3

32a+4b = 6

2(16a+2b) = 6

16a+2b = 6/2

16a+2b = 3 .... we'll use this later

Plug that value of c into the third equation as well

64a+8b+c = 0

64a+8b+(-4a-2b+3) = 0

60a+6b+3 = 0

3(20a+2b+1) = 0

20a+2b+1 = 0

20a+2b = -1

--------------------------

We have a new system of equations. This time it deals with 2 variables instead of 3. We can think of this as a reduced equivalent system.

`\begin{cases}16a+2b = 3\\20a+2b = -1\end{cases}`

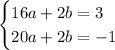
Note how subtracting the terms straight down has the b terms canceling (since 2b-2b = 0b = 0)

The 'a' terms subtract to 16a-20a = -4a

The terms on the right hand side subtract to 3-(-1) = 3+1 = 4

We end up with the equation -4a = 4 which solves to a = -1

Use this value of 'a' to find b

16a+2b = 3

16(-1)+2b = 3

-16+2b = 3

2b = 3+16

2b = 19

b = 19/2

b = 9.5

Now use the values of a and b to find c

4a+2b+c = 3

4(-1)+2(9.5)+c = 3

-4+19+c = 3

15+c = 3

c = 3-15

c = -12

--------------------------

Summary:

The values of a,b,c we found were

• a = -1
• b = 19/2 = 9.5
• c = -12

So the function is

f(x) = -x^2 + (19/2)x - 12

which is equivalent to

f(x) = -x^2 + 9.5x - 12

To check this answer, plug in x = 2, x = 6, x = 8 one at a time. You should get y = 3, y = 9 and y = 0 in that order.

Answer 2

f(x)=-x^2+9.5-12

Explanation:

- for the first box

9.5 for the second box

-12 for the third box