Answer: Yes, this trinomial -4(4t² -9t + 2) is factorable.
It is h =(-4)(4t -1 )(t -2) converted from the explanation
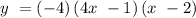
A graph of the equation is in the attachment. There are two equations, but only one graphed parabola because they are identical.
Step-by-step explanation: I am using x in place of t in this explanation, and leaving out the factored (-4) to simplify.
Using the systematic new AC Method to factor trinomials (Socratic Search) Starting with a quadratic equation in the form
y = ax² + bx + c
This involves converting the equation by multiplying the leading coefficient, a, times the constant, c
y =4x² –9x + 2
=4(x + p)(x + q)
Converted trinomial:
y' = x² –9x + 8
= (x + p')(x + q').
Here p' and q' will have the same – signs because the b term is negative and the c term is positive.
Factor pairs of ac = 8 are -1 and –8. This sum is –9 = b. Then p' = -1 and q' = -8.
Then divide the second factor by the original coefficient, 4.
Replacing the original leading factor (-4) the factored equation looks like
y = -4(4x - 1)(x - 2)
To solve for x
p =p’/a = ¼ or 4x - 1 = 0 4x = 1 x = ¹/₄
and
q ='q/a
= 8/4 = 2 OR x -2 = 0 x = 2
The second attachment shows some other ways to set up the equation without the (-4) to solve, and then replace that factor. You get the same values for x.
I hope this helps and is not too confusing. There may be other ways to factor this equation.