Question

Please explain thanks

Answer 1

`\large\boxed{\pink{\sf \leadsto Value \ of \ LM \ is \ 11 \ units . }}`

Explanation:

A figure is given to us in which we can see two triangles one is ∆ MPL and other is ∆MPN .

Figure :-

`\setlength{\unitlength}{1 cm}\begin{picture}(12,12)\linethickness{0.25mm}\put(0,0){\line(1,2){2}} \put(0.001,0){\line(1,0){4}}\put(2,0){\vector(0,1){5}}\put(4,0){\line( - 1,2){2}}\put(0,-0.4){$\bf L $}\put(2,-0.4){$\bf P$}\put(4,-0.4){$\bf N $}\put(2.2,4){$\bf M $}\put(2.8, - .4){$\bf 5 $}\put(1, - .4){$\bf 5 $}\put(3.4, 2){$\bf 11 $}\put(2.3,0){\line(0,1){.3}}\put(2.3,.3){\line( - 1,0){.3}}\end{picture}`

`\underline{\blue{\sf In\: \triangle MPL \ \& \ \triangle MPN :- }}`

`\qquad \bullet LP = PN = 5 \:\:(given) \\\\\qquad \bullet MP = MP \:\:(Common) \\\\\qquad \bullet \angle MPN = \angle MPL = 90^(\circ) \:\: (given)`

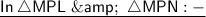
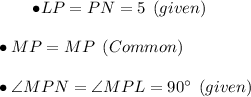
Hence by SAS congruence condition ,

`\orange{\bf \triangle MPL \cong \triangle MPN }`

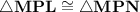
Hence by cpct ( Corresponding parts of congruent triangles ) we can say that , LM = NM = 11 units .

Hence the value of LM is 11 units .