Answer:

Explanation:
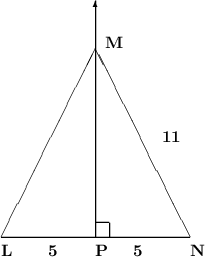
A figure is given to us in which we can see two triangles one is ∆ MPL and other is ∆MPN .
Figure :-
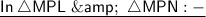
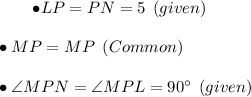
Hence by SAS congruence condition ,
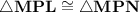
Hence by cpct ( Corresponding parts of congruent triangles ) we can say that , LM = NM = 11 units .
Hence the value of LM is 11 units .