Answer:
x ∈ (-∞, -2) ∪ (2, ∞)
Explanation:
To solve this problem we must factor the expression that is shown in the denominator of the inequality.
So, we have:
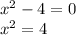
So the roots are:
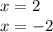
Therefore we can write the expression in the following way:
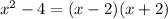
Now the expression is as follows:
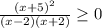
Now we use the study of signs to solve this inequality.
We have 3 roots for the polynomials that compose the expression:
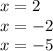 .
.
Observe the attached image.
We know that the first two roots are not allowed because they make zero the denominator, we also know that (x + 5) ^ 2 is always positive because it is squared, so it is not necessary to include the numerator in the study of signs.
Note that:
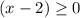 when
when
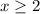
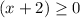 when
when
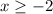
Finally after the study of signs we can reach the conclusion that:
x ∈ (-∞, -2) ∪ (2, ∞)