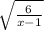Answer:
D.
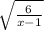
Explanation:
Given:

We can write
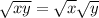
Using this property we can rewrite the given expression as
=
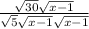
Now we can simplify √30/√5 = √6 and we can cancel out √(x - 1) both in the numerator and in the denominator, so we get
=
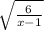
Therefore, the answer is D.