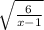Question

Which choice is equivalent to the quotient shown here for acceptable values of x

Answer 1

D.
`\sqrt(6)/(x-1)`

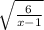
Explanation:

Given:

`(√(30(x-1)) )/(√(5(x-1)^2) )`

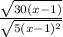
We can write
`√(xy) = √(x) √(y)`

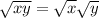
Using this property we can rewrite the given expression as

=
`(√(30)√(x-1)  )/(√(5) √(x-1)√(x-1)  )`

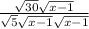
Now we can simplify √30/√5 = √6 and we can cancel out √(x - 1) both in the numerator and in the denominator, so we get

=
`\sqrt(6)/(x-1)`

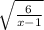
Therefore, the answer is D.
`\sqrt(6)/(x-1)`

Answer 2

D

Explanation:

Using the rule of radicals

`(√(a) )/(√(b) )` ⇔
`\sqrt{(a)/(b) }`

given

`(√(30(x-1)) )/(√(5(x-1)^2) )`

=
`\sqrt{(30(x-1))/(5(x-1)^2) }`

[ cancel 30 and 5 by 5 and (x - 1) / (x - 1)² by (x - 1) ]

=
`\sqrt{(6)/(x-1) }` → D