Given:
Consider the three point of second line are S, R, V instead of S, R, W.
A line with points T, R, W intersects a line with points S, R, V at point R. Another line extends from point R to point U between angle T, R, V.
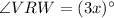
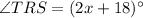
To find:
The m∠SRW.
Solution:
The figure according to the given information is shown below (not to scale).
From the below figure it is clear that,
 and
and
 are vertically opposite angles. So, their measures are equal.
are vertically opposite angles. So, their measures are equal.
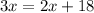
Subtract 2x from both sides.
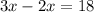
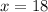
Using x=18 the measure of angle VRW is
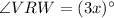

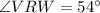
Now,
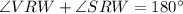 [Linear pair]
[Linear pair]
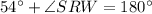

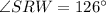
Therefore, the correct option is C.