Question

Triangle XYZ, X equals 27 cm, Y equals 79 cm and angle C equals 142Degrees. Find the length of Z, to the nearest centimeter.

Answer 1

Answer:102

Explanation:

Answer 2

Given:

In triangle XYZ, x = 27 cm, y = 79 cm and
`\angle C=142^\circ`.

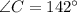To find:

The length of z.

Solution:

In triangle XYZ, using the Law of cosine, we get

`z^2=x^2+y^2-2xy\cos Z`

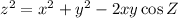
Putting the given values in the above formula, we get

`z^2=(27)^2+(79)^2-2(27)(79)\cos (142^\circ)`

`z^2=729+6241-4266(-0.788)`

`z^2=6970+3361.608`

`z^2=10331.608`

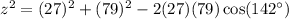
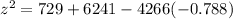
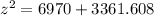
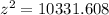
Taking square root on both sides.

`z=\pm √(10331.608)`

`z=\pm 101.6445178`

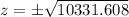
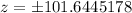
Approx the above value to the nearest number and side length cannot be negative. So,

`z\approx \pm 102\text{ cm}`

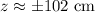
Therefore, the length of z is about 102 cm.