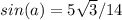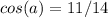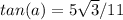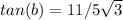Answer:
1)
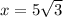
2)
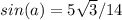

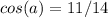

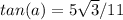
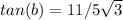
Explanation:
The Pythagorean Theorem is:

Where a is the hypotenuse and b and c are the legs.
The missing side lenght is one of the legs, then you must solve for one of them. Therefore, this is:
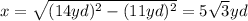
MEASURE OF ANGLE:
Keep the identities on mind:
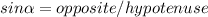
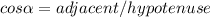
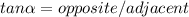
Susbstitute values, then: