Question

Line segment XY has endpoints X(–10, –1) and Y(5, 15). To find the y-coordinate of the point that divides the directed line segment in a 5:3 ratio, the formula y = (A/A+B) (y2 – y1) + y1 was used to find that y = (5/5+3) (15 – (–1)) + (–1).

Therefore, the y-coordinate of the point that divides XY into a 5:3 ratio is?

Answer 1

The y-coordinate is 9.

Explanation:

The given line segment has endpoints X(-10,-1) and Y(5,15).

The formula for finding the y-coordinate of the point that divides the directed line segment in the ratio a:b is

`y=((a)/(a+b) )(y_2-y_1)+y_1`.

The given ratio is 5:3.

We plug in the values to get

`y=((5)/(5+3))(15-(-1))+(-1)`

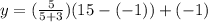
We simplify to get;

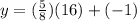
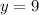`y=((5)/(8))(16)+(-1)`

`y=10-1`

`y=9`.

Answer 2

The y co-ordinate is 9

Explanation:

We simplify the expression given by the formula;

`(5)/(8)*16-1=9`