Question

Galileo wanted to release a wooden ball and an iron ball from a height of 100 meters and measure the duration of their fall. He found a plane with an incline of 12 degrees that degrees that he could climb until he could get to an altitude of 100 m. How far should Galileo walk up the inclined plane?

Answer 1

he would need to climb 480.97 m

Answer 2

He would need to climb 480.97 m

Step-by-step explanation:

The ground, the plane to climb and the altitude (100 m) all form a right-angled triangle

Therefore, we can apply the special trig functions.

These functions are as follows:

sin(θ) =
`(opposite)/(hypotenuse)`

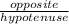
cos(θ) =
`(adjacent)/(hypotenuse)`

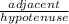
tan(θ) =
`(opposite)/(adjacent)`

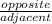
From the diagram, we have:

θ = 12°

The distance that he needs to climb is the hypotenuse

The altitude = 100 m is the opposite

Therefore, we can use the sin function as follows:

sin(12°) =
`(100)/(hypotenuse)`

hypotenuse =
`(100)/(sin(12))`

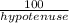
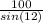
hypotenuse = 480.97 meters to the nearest hundredth

Therefore, he would need to climb 480.97 meters

Hope this helps :)