Question

Determine all numbers at which the function is continuous.

Answer 1

Answer: Option a.

Explanation:

Make the denominator equal to zero and solve for x, as following:

`x^(2)+8x-9=0`

To solve the quadratic equation you can factor ir. You must find two numbers whose sum is 8 and whose product is 9. These would be -1 and 9.

Then you have:

`(x-1)(x+9)=0\\x=1\\x=-9`

Therefore, based on this, you can conclude that the function is continuous at everty real number except x=1 and x=-9.

Answer 2

Option A. is the correct option.

Explanation:

In this question the given function is

`f(x)=(x^(2)+5x-36)/(x^(2)+8x-9)`

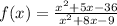
We have to find the continuity of the given function

If we rewrite the function in the factorial form

`f(x)=(x^(2)+9x-4x-36)/(x^(2)+9x-x-9)`

`=(x(x+9)-9(x+9))/(x(x+9)-1(x+9))`

`f(x)=((x+9)(x-9))/((x+9)(x-1))`

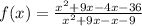
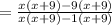
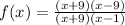
Now we take the denominator of the function

(x + 9) = 0

x = -9

and (x -1) = 0

x = 1

So for x = -9 and x = 0 the function becomes undefined.

Therefore function is continuous for every real number except x = -9 and x = 1.

Option a is the answer.