Question

The graphs of f(x) and g(x) are shown below. math

Answer 1

The correct option is 2.

Explanation:

From the given graphs in is clear that

`f(x)=x-3`

`g(x)=-0.5x`

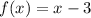
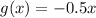
we need to find the interval for which (f-g)(x) is negative.

`(f-g)(x)=f(x)-g(x)`

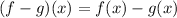
Substitute the values of both functions.

`(f-g)(x)=x-3-(-0.5x)`

`(f-g)(x)=x-3+0.5x`

`(f-g)(x)=1.5x-3`

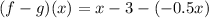
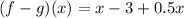
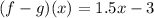
The value of (f-g)(x) is negative mean the value (f-g)(x) is less than 0.

`1.5x-3<0`

Add 3 on both sides.

`1.5x<3`

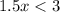
Divide both sides by 1.5.

`(1.5x)/(1.5)<(3)/(1.5)`

`x<2`

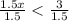
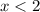
For all x<2, the value (f-g)(x) is negative. It means for the interval (-∞,2) the value (f-g)(x) is negative.

Therefore the correct option is 2.

Answer 2

Answer: SECOND OPTION.

Explanation:

1. You must subtract the function f(x) and g(x), therefore, you obtain:

`(f-g)(x)=x-3-(-0.5x)\\(f-g)(x)=x-3+0.5x\\(f-g)(x)=1.5x-3`

2. When you graph
`(f-g)(x)=1.5x-3`, you obtain the graph shown attached.

3. As you can see, the interval in which the value
`(f-g)(x)` is negative is:

(-∞,2)

Therefore the answer is the second option.