Answer:
The approximate value of the vehicle 13 years after purchase is $15827.
Explanation:
The formula for the value lost of an asset after n years, with depreciation rate r(in decimal) is given by:
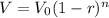
In which
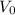 is the initial value.
is the initial value.
In this problem, we have that:
A vehicle purchased for $22400 depreciates at a constant rate of 9%. This means that
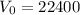 and
and
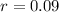 .
.
Determine the approximate value of the vehicle 13 years after purchase.
This means that
 .
.
So
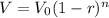
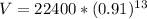
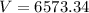
So, the approximate value of the vehicle 13 years after purchase is $22400 - $6573 = $15827.