4. A random variable X has a mean of 10 and a standard deviation of 3. If 2 is added to each value of X, what will the new mean and standard deviation be?

Question

asked Sep 16, 2020 166k views

1 Answer

Nicolas Cortot · Answer 1 · 2020-09-23T04:42:01+0000

Adding 2 to each value of the random variable
makes a new random variable
X+2 . Its mean would be

E[X+2]=E[X]+E[2]=E[X]+2

since expectation is linear, and the expected value of a constant is that constant.
E[X] is the mean of
, so the new mean would be

E[X+2]=10+2=12

The variance of a random variable
is

V[X]=E[X^2]-E[X]^2

so the variance of
X+2 would be

V[X+2]=E[(X+2)^2]-E[X+2]^2

We already know
E[X+2]=12 , so simplifying above, we get

V[X+2]=E[X^2+4X+4]-12^2

V[X+2]=E[X^2]+4E[X]+4-12^2

V[X+2]=(V[X]+E[X]^2)+4E[X]-140

Standard deviation is the square root of variance, so
V[X]=3^2=9 .

$\implies V[X+2]=(9+10^2)+4(10)-140=9$

so the standard deviation remains unchanged at 3.

NB: More generally, the variance of
aX+b for
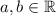$a,b\in\mathbb R$ is

V[aX+b]=a^2V[X]+b^2V[1]

but the variance of a constant is 0. In this case,
a=1 , so we're left with
V[X+2]=V[X] , as expected.