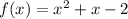QUESTION 1
The given binomial is;
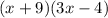
First terms are multiplied:
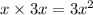
Outside terms are multiplied:

Inside terms are multiplied:
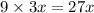
Last terms are Multiplied:
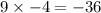
This gives us;

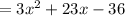
QUESTION 2
We want to factor
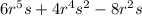
The HCF is
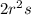
We factor to get;
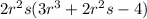
QUESTION 3;
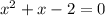
Split the middle term;
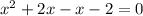
Factor
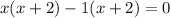
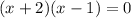
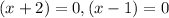
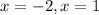
The solutions are;
 and
and

These are the x-intercepts of the graph of the function