Answer:
a. 2
Explanation:
The given function is
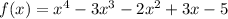 .
.
We can see from the graph that the graph has two x-intercepts.
This means that the function has two real zeros.
By the fundamental theorem of Algebra, the function is supposed have four roots since it is a polynomial of degree 4.
Therefore, the other two zeros are complex.
See graph