Answer:
Hence, the limit of the expression
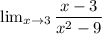 is:
is:
0.1667 (i.e. option b is true)
Explanation:
We are asked to estimate the limit of the expression:
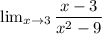
We know that:
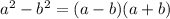
Hence, we could represent it as:
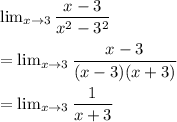
Since we cancel out the similar terms in the numerator as well as in the denominator.
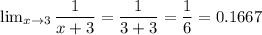
Hence, the limit of the expression
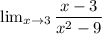 is:
is:
0.1667