Question

Estimate the limit.
Picture below

Answer 1

what is it

Explanation:

Answer 2

Hence, the limit of the expression:
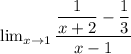`\lim_(x \to 1) ((1)/(x+2)-(1)/(3))/(x-1)` is:

`(-1)/(9)`

Explanation:

We are asked to estimate the limit of the expression:

`\lim_(x \to 1) ((1)/(x+2)-(1)/(3))/(x-1)`

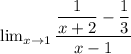
We will simplify the expression by first taking the l.c.m of the terms in the numerator to obtain the expression as:

`(3-(x+2))/(3(x+2))\\\\=(3-x-2)/(3(x+2))\\\\=(1-x)/(3(x+2))`

`\lim_(x \to 1) (1-x)/(3(x+2)(x-1))\\\\= \lim_(x \to 1) (-(x-1))/(3(x+2)(x-1))\\\\\\= \lim_(x \to 1) (-1)/(3(x+2))`

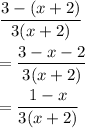
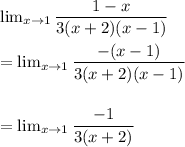
since the same term in the numerator and denominator are cancelled out.

Now the limit of the function exist as the denominator is not equal to zero when x→1.

Hence,

`\lim_(x \to 1) (-1)/(3(x+2))\\\\=(-1)/(3(1+2))\\\\=(-1)/(3* 3)\\\\=(-1)/(9)`

Hence, the limit of the expression:
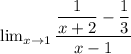`\lim_(x \to 1) ((1)/(x+2)-(1)/(3))/(x-1)` is:

`(-1)/(9)`