Question

There are 10 cars in today’s Grand Prix race in how many different ways can three cars win first second and third places

Answer 1

The number of ways it could be done is:

720

Explanation:

It is given that:

There are 10 cars in today’s Grand Prix race.

We have to find the different number of ways these three cars win first second and third places.

That is we have to choose the three cars and arrange them in ways as according to they obtain there ranks.

Hence, we will use the method of permutation since we have to choose three cars and also arrange them according to their order they finished the race and took first, second and third place.

Hence, the number of ways it could be done is:

`n_P_(r)=(n!)/((n-r)!)`

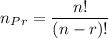
Here we have n=10 and r=3.

Hence,

`10_P_(3)=(10!)/((10=3)!)\\\\\\10_P_3=(10!)/(7!)\\\\\\10_P_3=10* 9* 8\\\\\\10_P_3=720`

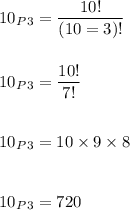
Hence, the number of ways it could be done is:

720