Question

a car purchased for $34,000 is expected to lose value, or depreciate, at a rate of 6% per year.using x for years and y for the value of the car, write the equation that models this situation.after how many years is the car first worth less than $21,500?

Answer 1

`y = 34000(1-0.06) ^ t`

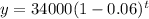
After 7.40 years it will be worth less than 21500

Explanation:

This problem is solved using a compound interest function.

This function has the following formula:

`y = P(1-n) ^ t`

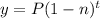
Where:

P is the initial price = $ 34,000

n is the depreciation rate = 0.06

t is the elapsed time

The equation that models this situation is:

`y = 34000(1-0.06) ^ t`

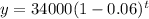
Now we want to know after how many years the car is worth less than $ 21500.

Then we do y = $ 21,500. and we clear t.

`21500 = 34000(1-0.06) ^ t\\\\log(21500/34000) = tlog(1-0.06)\\\\t = (log(21500/34000))/(log(1-0.06))\\\\t = 7.40\ years.`

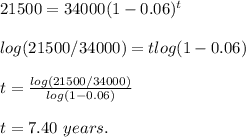
After 7.40 years it will be worth less than 21500