Question

A water balloon launcher uses an elastic band with a spring constant of 115 N/m. To use the launcher, you stretch the band back with a balloon in it. The water balloons have a mass of 1.3 kg/

a. If you stretch the band by 0.8 m, what elastic force will the band exert?

b. With the band stretched 0.8 m, how much elastic potential energy is stored in the spring?

c. If you release the band, it pushes the balloon forward. What is the kinetic energy of the balloon when it reaches the natural length of the band? Explain how you found the answer.

d. What is the speed of the balloon when it reaches the natural length of the band?

Answer 1

a) F=kx=92 N

b) PE=1/2*k*x^2=36.8 J

c) Apply law of conservation of energy:

KE=PE=1/2*m*v^2=36.8 J

d)
`v=\sqrt{(2KE)/(m)}=7.52` m/s

Answer 2

Here elastic balloon launcher will behave like an ideal spring

so here we have

spring constant k = 115 N/m

mass of balloon = 1.3 kg

Part a)

Stretch in the band is given as

x = 0.8 m

now the force on the balloon is given by

F = k x

now from above

`F = (115) (0.8) = 92 N`

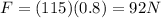
so it will exert 92 N force on it

Part b)

Elastic potential energy is given as

`U = (1)/(2)kx^2`

so here we have

`U = (1)/(2)(115)(0.8)^2`

`U = 36.8 J`

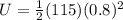
Part c)

Here in this case we can say that kinetic energy gained by the balloon must be same as the elastic potential energy stored in the rubber because there is no energy loss in this system

So kinetic energy = 36.8 J

Part d)

As we know by the formula of kinetic energy

`K = (1)/(2)mv^2`

`36.8 = (1)/(2)(1.3)v^2`

`v = 7.52 m/s`

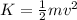
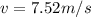
so speed of the balloon will be 7.52 m/s