Question

Determine any data values that are missing from the table, assuming that the data represent a linear function.

X Ix ly |-12 17 -10 19 -8 23

a. Missing x:-6 Missing y:22
b. Missing x:-7 Missing y:22
c. Missing x:-7 Missing y:20
d. Missing x:-6 Missing y:21

Please select the best answer from the choices provided Save and Exit Next Submit Mark this and return​

Answer 1

the answer is?

Explanation:

Answer 2

we conclude that:

• The value of missing x = 6

• The value of missing y = 21

Explanation:

Given that the table represents a linear function, so the function is a straight line.

Taking two points

• (-12, 17)

• (-10, 19)

Finding the slope between (-12, 17) and (-10, 19)

`\mathrm{Slope}=(y_2-y_1)/(x_2-x_1)`

`\left(x_1,\:y_1\right)=\left(-12,\:17\right),\:\left(x_2,\:y_2\right)=\left(-10,\:19\right)`

`m=(19-17)/(-10-\left(-12\right))`

`m=1`

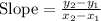
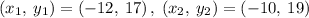
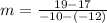
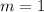
Using the point-slope form to determine the linear equation

`y-y_1=m\left(x-x_1\right)`

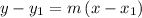
where m is the slope of the line and (x₁, y₁) is the point

substituting the values m = 1 and the point (-12, 17)

`y-y_1=m\left(x-x_1\right)`

`y - 17 = 1 (x - (-12)`

`y - 17 = x+12`

`y = x + 12+17`

`y = x+29`

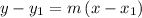
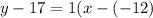
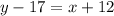
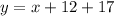
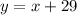
Thus, the equation of the linear equation is:

`y = x+29`

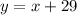
Now substituting x = -8 in the equation

`y = x+29`

`y = -8+29`

`y = 21`

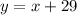
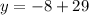
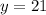
Thus, the value of missing y = 21 when x = -8

Now substituting y = 23 in the equation

`y = x+29`

`23 = x+29`

`x = 29 - 23`

`x = 6`

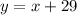
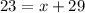
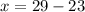
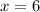
Therefore, the value of missing x = 6 when y = 23

Hence, we conclude that:

• The value of missing x = 6

• The value of missing y = 21