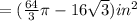Question

Express answer in exact form.

A segment of a circle has a 120 arc and a chord of 8√3 in. Find the area of the segment.

Please show work I am totally stuck on this.. Thank you (75 points)

Answer 1

`=((64)/(3)\pi-16√(3)) in^2`

Explanation:

Area of segment equals area of sector minus area of isosceles triangle.

`=(\theta)/(360)* \pi r^2 -(1)/(2) r^2 \sin(\theta)`

Given; the length of chord,
`d=8√(3) in.`

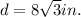
and the angle of the sector,
`\theta=120\degree`.

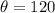We can use the formula for calculating the length of a chord to find the radius of the circle.

`d=2r\sin((\theta)/(2))`

`8√(3)=2r\sin(60\degree)`

`8√(3)=2r((√(3))/(2))`

`\Rightarrow r=8in.`

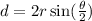
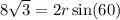
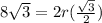
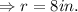
Area of segment
`=(120)/(360)* \pi * 8^2-(1)/(2)* 8^2\sin(120\degree)`

`=((64)/(3)\pi-16√(3)) in^2`