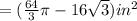Answer:
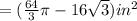
Explanation:
Area of segment equals area of sector minus area of isosceles triangle.
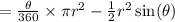
Given; the length of chord,
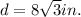
and the angle of the sector,
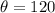 .
.
We can use the formula for calculating the length of a chord to find the radius of the circle.
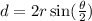
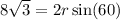
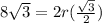
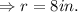
Area of segment