Question

how do the graphs of f(x) = sin x and g(x) = sin2x+3 compare. Must make two selections of the following that apply.

Answer 1

Answers are in image provided

Explanation:

I used the other persons answers and they got it wrong for me.

Answer 2

The correct options are:

• g(x) is shifted three units higher than f(x).

• g(x) has a period that is half the period of f(x).

Explanation:

We have to compare the graphs of the function:

`f(x)=\sin x`

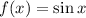
and
`g(x)=\sin 2x+3`

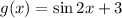
We have to select the correct options among the following:

As we know that the period of sine function is 2π.

i.e. Period of function f(x) is: 2π.

The period of sin(2 x) is π.

Hence, the period of the function g(x) function is π.

• Hence, the period of g(x) is half the period of f(x).

• Also we could observe that g(x) is shifted 3 units upward.