Question

Find the area of a triangle bounded by the y-axis, the line f(x)=12-4x, and the line perpendicular to (f) that passes through the origin.

Answer 1

`(288)/(17)\ un^2.`

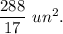
Explanation:

1. The line y=12-4x has the slope -4, then perpendicular line will have slope
`(1)/(4).`

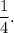
The equation of this perpendicular line is

`y-0=(1)/(4)(x-0),\\ \\4y=x.`

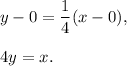
2. The vertices of the triangle are at points:

A: x=0, y=0.

B: x=0, y=12.

C:
`\left\{\begin{array}{l}y=12-4x\\4y=x\end{array}\right.\Rightarrow y=12-16y,\ y=(12)/(17),\ x=(48)/(17).`

3. The height of the triangle ABC is x-coordinate of point C, so
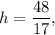`h=(48)/(17),` the base of the triangle is the length of the segment AB, 12 cm.

4. The area of the triangle ABC is
`(1)/(2)\cdot 12\cdot (48)/(17)=(288)/(17)\ un^2.`