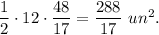Answer:
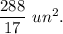
Explanation:
1. The line y=12-4x has the slope -4, then perpendicular line will have slope
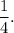
The equation of this perpendicular line is
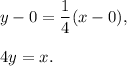
2. The vertices of the triangle are at points:
A: x=0, y=0.
B: x=0, y=12.
C:
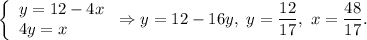
3. The height of the triangle ABC is x-coordinate of point C, so
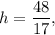 the base of the triangle is the length of the segment AB, 12 cm.
the base of the triangle is the length of the segment AB, 12 cm.
4. The area of the triangle ABC is