Answer:
The point C is (a,0)
C is correct.
Explanation:
If the coordinate axes contain two sides of a square ABCD such that A(0, a) and B(0, 0) are two vertices of the square.
ABCD is a square.
Vertex moves from
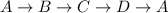
B is (0,0). For C we have to move either left or right on x-axis to reach at C.
A (0,a) and B(0,0)
Length of AB = a
Length of BC must be a
Because all sides of square is same length.
If we moves "a" unit left from origin then coordinate is (-a,0)
If we moves "a" unit right from origin then coordinate is (a,0)
Possible coordinate of C: (-a,0) or (a,0)
Hence, The point C is (a,0)