Answer:
Option a)
Explanation:
To get the vertical asymptotes of the function f(x) you must find the limit when x tends k of f(x). If this limit tends to infinity then x = k is a vertical asymptote of the function.
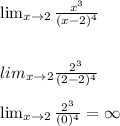
Then. x = 2 it's a vertical asintota.
To obtain the horizontal asymptote of the function take the following limit:
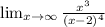
if
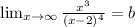 then y = b is horizontal asymptote
then y = b is horizontal asymptote
Then:
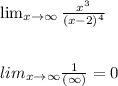
Therefore y = 0 is a horizontal asymptote of f(x).
Then the correct answer is the option a) x = 2, y = 0