Question

Determine the equations of the vertical and horizontal asymptotes, if any, for y=x^3/(x-2)^4

a) x=2, y=0

b) x=2

c) x=2, x=-2

d) x=2, y=1

Answer 1

ANSWER

The correct answer is A.

EXPLANATION

The given function is,


`y = \frac{ {x}^(3) }{ {(x - 2)}^(4) }`

To find the vertical asymptote, we equate the denominator to zero.

This implies that,


`{(x - 2)}^(4) = 0`


`x - 2 = 0`


`x = 2`

To find the horizontal asymptote,we take limit to infinity.


`lim_(x\rightarrow \infty) \frac{ {x}^(3) }{ {(x - 2)}^(4) } =0`

The horizontal asymptotes is


`y=0`

Answer 2

Option a)

Explanation:

To get the vertical asymptotes of the function f(x) you must find the limit when x tends k of f(x). If this limit tends to infinity then x = k is a vertical asymptote of the function.

`\lim_(x\to\\2)(x^3)/((x-2)^4) \\\\\\lim_(x\to\\2)(2^3)/((2-2)^4)\\\\\lim_(x\to\\2)(2^3)/((0)^4) = \infty`

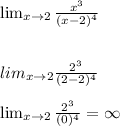
Then. x = 2 it's a vertical asintota.

To obtain the horizontal asymptote of the function take the following limit:

`\lim_(x \to \infty)(x^3)/((x-2)^4)`

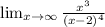
if
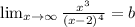`\lim_(x \to \infty)(x^3)/((x-2)^4) = b` then y = b is horizontal asymptote

Then:

`\lim_(x \to \infty)(x^3)/((x-2)^4) \\\\\\lim_(x \to \infty)(1)/((\infty)) = 0`

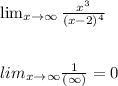
Therefore y = 0 is a horizontal asymptote of f(x).

Then the correct answer is the option a) x = 2, y = 0