Question

Given that domain is all real numbers, what is the limit of the range for the function f(x)=4^2x -100?

Answer 1

y>-100 is the range.

Explanation:

Given is the function f(x) with domain the set of all real numbers

`f(x)=4^(2x) -100`

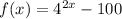
Let us substitute y =f(x)

`y=4^(2x) -100`

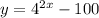
Let us solve x in terms of y to find the range

`y+100=4^(2x) \\2x log 4 = log (y+100)\\x = (log(y+100))/(2log4) \\x= (log(y+100))/(log16)`

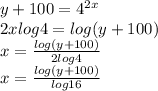
Since log is defined only for non negative positive numbers excluding 0, we have y+100>0

y>-100 is the range.