Question

Help me ASAP...........

Answer 1

Alternative B is the correct answer.

Explanation:

We have been given the following quadratic equation;

5x = 6x²-3. The first step is to re-arrange the equation and write the equation in standard form; ax²+bx+c = 0

6x²-5x-3 = 0 . This implies that; a = 6 , b = -5 and c = -3 . The quadratic formula is given as;

x =(-b±√b²-4ac) / 2a

Plugging in the values of a, b and c into the formula yields;

x = (-(-5)±√(-5)²-4(6)(-3) ) / 2(6)

x = (5±√25+72) / 12

x = (5±√97) / 12 which is the solution

Answer 2

Option (b) is correct.

`x=(5\pm√(97))/(12)`

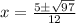
Explanation:

Given :
`5x=6x^2-3`

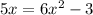
We have to solve using quadratic formula and find value for x.

Consider the given equation
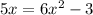`5x=6x^2-3` it can be rewritten as :
`6x^2-5x-3=0`

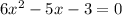
The standard form of quadratic equation is
`ax^2+bx+c=0` , and the quadratic formula for the standard equation is given by,

`x=(-b\pm√(b^2-4ac))/(2a)`

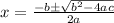
Compare the given equation with standard equation , we have a = 6 , b = -5 and c = -3.

Substitute in quadratic formula, we have,

`x=(5\pm√((5)^2-4\cdot 6\cdot (-3)))/(2(6))`

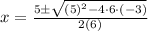
Simplify, we get,

`\Rightarrow x=(5\pm√(25+72))/(12)`

`\Rightarrow x=(5\pm√(97))/(12)`

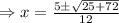
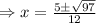
Thus, option (b) is correct.