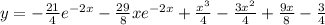By finding complementary solution and particular solution we got the
the solution of IVP as
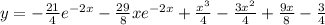
What is a differential equation?
An equation of function and their derivatives is called differential equation .
Given differential equation
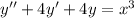
Homogenous equation can be written as
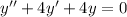
characteristic equation of this differential equation can be written as
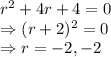
Roots are repeating
Hence we can write complementary solution as
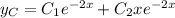
The functions that are making up this solution are
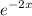 and
and

Now particular solution
Let suppose that particular solution is of the form
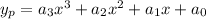
So
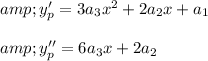
Putting these values in given differential equation
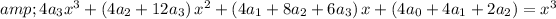
Now by comparing the coefficient of both sides

Hence we can write particular solution as
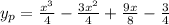
We know general solution
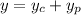
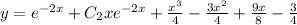
Now given initial values
 and
and
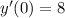
So
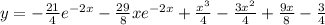
By finding complementary solution and particular solution we got the
the solution of IVP as