For this case, we have that by definition, two lines of the form y = f (x) are parallel if they have the same slope, that is:
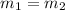
In this case we have the following line:
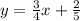
Your slope is:
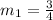
Then, a parallel line must have slope:
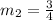
Then, the correct option is:
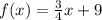
Answer:
Option A