2 Answers

Noha · Answer 1 · 2020-06-01T04:53:52+0000

For this case, we have that by definition, two lines of the form y = f (x) are parallel if they have the same slope, that is:

$m_ {1} = m_ {2}$

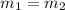
In this case we have the following line:

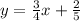
$y = \frac {3} {4} x + \frac {2} {5}$

Your slope is:

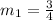
$m_ {1} = \frac {3} {4}$

Then, a parallel line must have slope:

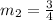
$m_ {2} = \frac {3} {4}$

Then, the correct option is:
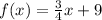
$f (x) = \frac {3} {4} x + 9$

Answer:

Option A

Please log in or register to add a comment.