Answer:
1. Perfect square trinomial on left sides is
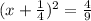 .
.
2. The equation after applying the square root property of equality is
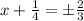 .
.
Explanation:
The given equation is
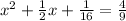
It can be written as
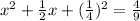
Factor the perfect-square trinomial on the left side of the equation.
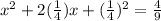
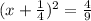
![[\because (a+b)^2=a^2+2ab+b^2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/a4ffb4tvrpo42nxyev3p27dcpol4fcd030.png)
Therefore the required equation is
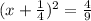
Taking square root both the sides.
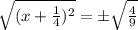
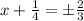
Therefore the equation after applying the square root property of equality is
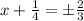 .
.