Question

Can someone please help???

Answer 1

Option A

Explanation:

We assume that after the first player and second player choose a card they do not return the card to the deck and that the events are mutually exclusive (ie, you can not get a queen and jack by selecting a single card).

It can be seen in the figure that there are 52 cards in the deck. It can be seen that there are 4 queens and 4 jacks.

Thus:

If the first player selected a jack, then there are only 3 jacks left in the deck, and 51 cards in total.

If the second player selected a queen, then there are only 3 queens left in the deck and 50 cards in total.

Therefore, the probability Pj that the third player selects a Jack

is
`P_(j) = (3)/(50)`

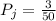
Then, the probability Pq that the third player selects a queen

is
`P_(q) = (3)/(50)`

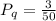
Finally the probability of selecting a jack or queen is:

P(j ∪ q) =
`P_(j) + P_(q)`

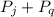
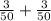
P(j ∪ q) =
`(3)/(50) + (3)/(50)`

P(j ∪ q) =
`(3)/(25)`.

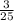The correct answer is the first option.