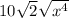Answer:
x>0 and working with real numbers
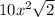
OR
x<0 and working with imaginary/complex numbers
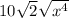
OR
Leave it like the following for both systems(Real/Complex) numbers
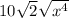
Explanation:
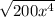
First simplify
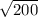
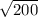
Find a perfect square and a non perfect square, which when you multiply the two squares it gives you
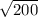
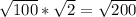
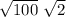
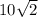
Now get the square root of
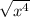 if we are working with real numbers and x > 0
if we are working with real numbers and x > 0
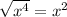
If x not > 0 then just leave as
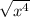
Now combine it all
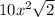
OR