Question

A vanilla thickshake is $2 more than a fruit juice. If 3 vanilla thickshakes and 5 fruit juices cost $30, determine their individual prices using simultaneous elimination

Answer 1

vanilla thickshake = $5

fruit juice = $3

Answer 2

USING ELIMINATION METHOD

Let the price of vanilla thickshake = x

Let the price of fruit juice = y

Given that a vanilla thickshake is $2 more than a fruit juice.

so

• x = 2+y ...... (Equation 1)

Given that If 3 vanilla thickshakes and 5 fruit juices cost $30.

• 3x+5y=30 ...... (Equation 2)

So the system of equations

`x = 2+y`

`3x+5y = 30`

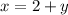
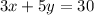
Arrange equation variables for elimination

`\begin{bmatrix}x-y=2\\ 3x+5y=30\end{bmatrix}`

`\mathrm{Multiply\:}x-y=2\mathrm{\:by\:}3\:\mathrm{:}\:\quad \:3x-3y=6`

`\begin{bmatrix}3x-3y=6\\ 3x+5y=30\end{bmatrix}`

so

`3x+5y=30`

`-`

`\underline{3x-3y=6}`

`8y=24`

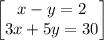
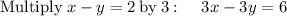
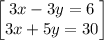
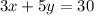
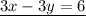
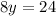
so the system of equations becomes

`\begin{bmatrix}3x-3y=6\\ 8y=24\end{bmatrix}`

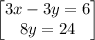
solve 8y = 24 for y

`8y=24`

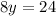
Divide both sides by 2

`(8y)/(8)=(24)/(8)`

`y=3`

`\mathrm{For\:}3x-3y=6\mathrm{\:plug\:in\:}y=3`

`3x-3\cdot \:3=6`

`3x-9=6`

`3x=15`

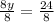
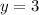
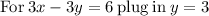
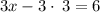
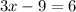
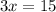
Divide both sides by 3

`(3x)/(3)=(15)/(3)`

`x=5`

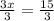
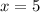
Therefore,

• The price of fruit juice = y = 3

• The price of vanilla thickshake = x = 5

2ND METHOD

Explanation:

• Let the price of fruit juice = x

As a vanilla thickshake is $2 more than a fruit juice.

• Thus the price of thickshake vanilla = x+2

Given that 3 vanilla thickshakes and 5 fruit juices cost $30.

3(Vanilla thickshakes) + 5(fruit juice) = 30

3(x+2) + 5x = 30

3x+6+5x=30

8x+6=30

8x=30-6

8x=24

x = 3

Thus,

• The price of fruit juice = x = $3

• The price of vanilla thickshake = x+2 = 3+2 = $5