USING ELIMINATION METHOD
Let the price of vanilla thickshake = x
Let the price of fruit juice = y
Given that a vanilla thickshake is $2 more than a fruit juice.
so
- x = 2+y ...... (Equation 1)
Given that If 3 vanilla thickshakes and 5 fruit juices cost $30.
- 3x+5y=30 ...... (Equation 2)
So the system of equations
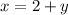

Arrange equation variables for elimination
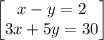
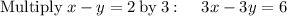
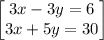
so
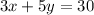

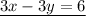
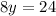
so the system of equations becomes
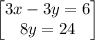
solve 8y = 24 for y
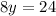
Divide both sides by 2
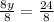
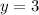
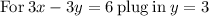
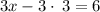
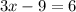
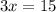
Divide both sides by 3
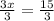

Therefore,
- The price of fruit juice = y = 3
- The price of vanilla thickshake = x = 5
2ND METHOD
Explanation:
- Let the price of fruit juice = x
As a vanilla thickshake is $2 more than a fruit juice.
- Thus the price of thickshake vanilla = x+2
Given that 3 vanilla thickshakes and 5 fruit juices cost $30.
3(Vanilla thickshakes) + 5(fruit juice) = 30
3(x+2) + 5x = 30
3x+6+5x=30
8x+6=30
8x=30-6
8x=24
x = 3
Thus,
- The price of fruit juice = x = $3
- The price of vanilla thickshake = x+2 = 3+2 = $5