Answer:
Value of cosθ is ±√7/3 .
Explanation:
According to the Question , value of :
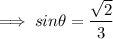
And , we know the identity of sine and cosine as ,
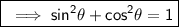
Using , this identity we have ;
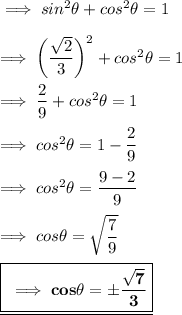
Now , here since θ is in 2nd quadrant and in 2nd quadrant cos is negative . Hence ,the value of cos will be :
