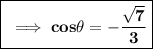Question

What is cos theta when sin theta = sqrt 2/3

Answer 1

Value of cosθ is ±√7/3 .

Explanation:

According to the Question , value of :

`\red{\implies sin\theta = (\sqrt2)/(3)}`

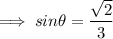
And , we know the identity of sine and cosine as ,

`\boxed{\pink{\sf\implies sin^2\theta + cos^2\theta = 1} }`

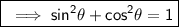
Using , this identity we have ;

`\implies sin^2\theta + cos^2\theta = 1 \\\\\implies \bigg( (\sqrt2)/(3)\bigg)^2 + cos^2\theta = 1 \\\\\implies (2)/(9) + cos^2\theta = 1 \\\\\implies cos^2\theta = 1 - (2)/(9) \\\\\implies cos^2\theta = (9-2)/(9) \\\\\implies cos\theta = \sqrt{(7)/(9)} \\\\\underline{\boxed{\blue{\bf \implies cos\theta = \pm (\sqrt 7 )/(3)}}}`

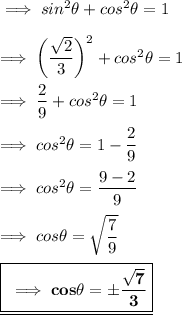
Now , here since θ is in 2nd quadrant and in 2nd quadrant cos is negative . Hence ,the value of cos will be :

`\boxed{\orange{\bf \implies cos\theta =-(\sqrt7)/(3)}}`